Método de ortogonalización de Gram-Schmidt
En matemáticas y análisis numérico, el método de ortogonalización de Gram–Schmidt de álgebra lineal es un método de ortogonalizar un conjunto de vectores en un espacio prehilbertiano, más comunmente el espacio euclídeo Rn. Ortogonalización en este contexto significa lo siguiente: comenzamos con vectores v1,…, vk los cuales son linealmente independientes y queremos encontrar mutuamente vectores ortogonales u1, …, uk los cuales generan el mismo subespacio que los vectores v1, …, vk.
Si tenemos una base en V,
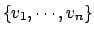 podemos pasar a partir de ella a una base que es ortonormal
podemos pasar a partir de ella a una base que es ortonormal 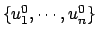 . El proceso que se sigue es el siguiente: Comenzamos con un vector de la base
. El proceso que se sigue es el siguiente: Comenzamos con un vector de la base 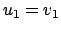 , dividimos por su norma y ya lo tenemos de norma 1.
, dividimos por su norma y ya lo tenemos de norma 1.Consideramos ahora otro vector de la base, V2 y tomamos uno ortogonal a . Por definición
. Por definición





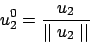








No hay comentarios:
Publicar un comentario