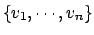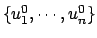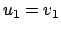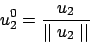2. Todo subespacio vectorial W de V tiene asimismo estructura de espacio vectorial con las mismas operaciones que V .
Diremos que un vector v 2 V es combinación lineal de la familia S = {v1, . . . , vm} � V si v =
a1v1 + · · · + amvm con ai 2 K para todo i = 1, . . . ,m.
Sea S un subconjunto del espacio vectorial V y sea L(S) el conjunto formado por todas las combinaciones lineales de elementos de S.
L(S) = {a1v1 + · · · + amvm tal que m 2 N, vi 2 S, ai 2 K, i = 1, . . . ,m}
Al conjunto L(S) se le llama envolvente lineal de S o subespacio generado por S y es el menor
subespacio vectorial de V que contiene al conjunto S, esto es, si S � W, con W un subespacio
vectorial de V , entonces L(S) � W.
1.2. DEPENDENCIA E INDEPENDENCIA LINEAL. BASES.
Definición 4. (Dependencia e independencia lineal)
Sea V un K-espacio vectorial y sean v1 . . . , vm 2 V . Se dice que la familia de vectores S =
{v1, . . . , vm} es linealmente dependiente si existen a1, . . . , am 2 K, no todos nulos, tales que
a1v1 + a2v2 + · · · + amvm =¯0
o, dicho de otro modo, si existe un vector vi 2 S que se puede poner como combinación lineal del resto.
Se dice que el conjunto de vectores S = {v1, . . . , vm} es linealmente independiente si no es linealmente dependiente, esto es, de ser cierta la igualdad
a1v1 + a2v2 + · · · + amvm =¯0, entonces a1 = · · · = am = 0. Esto equivale a decir que ningún vector de S se puede poner como combinación lineal del resto.
Ejemplo 4. Dependencia e independencia lineal.
Observación 3. 1. {v1} es l.i. (linealmente independiente) si y sólo si v1 6=¯0.
2. Si {v1, . . . , vm} es l.d. (linealmente dependiente), entonces
{v1, . . . , vm, vm+1, . . . , vm+r}
también es l.d..
3. Si {v1, . . . , vm, vm+1, . . . , vm+r} es l.i., entonces {v1, . . . , vm} es l.i..
Definición 5. (Sistema de generadores)
Un conjunto de vectores S � V es un sistema de generadores del espacio vectorial V si L(S) = V .
Propiedades.
1. Si S = {v1, . . . , vm} es un sistema de generadores de V , con vi combinación lineal de los restantes
vectores, entonces {v1, . . . , vi−1, vi+1, . . . , vm} es también un sistema de generadores de V .
2. Si {v1, . . . , vm} son l.i., entonces cualquier sistema de generadores de V tendrá, al menos, m
elementos.
Ejemplo 5. Sistemas de generadores.
Definición 6. (Base)
Una familia de vectores B � V es una base del espacio vectorial V si es linealmente independiente
y sistema de generadores de V .
Si V admite una base finita B = {v1, . . . , vn} de n vectores, lo llamaremos espacio vectorial de
dimensión finita. Diremos que la dimensión de V es n, dim(V ) = n.
2
Propiedades. Sea V un espacio vectorial de dimensión finita n. Entonces:
1. Cada vector v 2 V se podrá escribir de modo único como combinación lineal de los elementos de
cualquier base.
2. (Teorema de la base) Todas las bases de V tienen n vectores.
3. (Teorema de ampliación de la base) Sea S = {v1, . . . , vm} una familia de vectores l.i. de V .
Entonces S se puede ampliar a otra {v1, . . . , vm, vm+1, . . . , vn} que es una base de V .
4. Si S = {v1, . . . , vn} son n vectores de V linealmente independientes, entonces son también base
de V .
5. Si S = {v1, . . . , vm} contiene más de n vectores, S es linealmente dependiente.
6. Si S = {v1, . . . , vm} es sistema de generadores de V , cualquier número máximo de vectores
linealmente independientes de S es base de V .
7. Una familia de vectores S = {v1, . . . , vm} � V es base de un subespacio vectorial W � V si S es
linealmente independiente y L(S) = W.
Ejemplo 6. Bases.
1.3. SUBESPACIO GENERADO POR LAS FILAS DE UNA MATRIZ. OBTENCIÓN
DE LA BASE DE UNA ENVOLVENTE LINEAL.
Sea A 2 Mm×n(K). Las filas de A,
A1 = (a11, . . . , a1n), . . . ,Am = (am1, . . . , amn)
pueden verse como vectores de Kn y, por tanto, podemos decir que generan un subespacio de Kn
llamado espacio fila de A y que denotamos por F(A), esto es,
F(A) = L(A1, . . . ,Am)
Propiedades.
1. Si al realizar operaciones elementales sobre las filas de A obtenemos una nueva matriz B, entonces
F(A) = F(B).
2. Si E es una matriz escalonada asociada a A, entonces los vectores fila no nulos de E son base de
F(A) = F(E).
3. Para saber si dos subespacios engendrados por dos familias de vectores de Kn son iguales basta
ver si las dos matrices cuyas filas son las coordenadas de los vectores de las dos familias dan lugar
a la misma matriz escalonada reducida.
4. El rango de una matriz A 2 Mm×n(K) coincide con el número máximo de vectores fila l.i. (la
dimensión de F(A)), y con el número máximo de vectores columna l.i.
Ejemplo 7. Obtención de la base de una envolvente lineal.
1.4. ECUACIONES CARTESIANAS Y PARAMÉTRICAS DE UN SUBESPACIO.
Dado un sistema homogéneo de m ecuaciones con n incógnitas (I) A¯x = ¯0, con A 2 Mm×n(K), y
dado el conjunto W = {soluciones de (I)}, a (I) lo llamaremos ecuaciones cartesianas (o implícitas) de
W.
Propiedades.
1. W es un subespacio vectorial de Kn con dim(W) = n − r siendo r el rango de A.
3
2. El sistema homogéneo (II) B¯x = ¯0 con B una matriz obtenida de A mediante operaciones
elementales sobre las filas es equivalente a (I), esto es, tiene las mismas soluciones. Reduciremos
el problema de resolver (I) al de resolver (II) E¯x =¯0 con E una matriz escalonada asociada a A.
Ejemplo 8. Sistemas homogéneos. Sistemas equivalentes.
Sea W un subespacio vectorial de Kn con dim(W) = m � n y sea BW = {w1, . . . ,wm} una base
de W con wi = (a1i, a2i, . . . , ani) para i = 1, . . . ,m. Entonces cualquier vector x = (x1, . . . , xn) 2 W
se escribe como (x1, . . . , xn) = �1(a11, . . . , an1) + · · · + �m(a1m, . . . , anm).
Si igualamos las coordenadas, quedan las ecuaciones paramétricas de W
8>
<>
:
x1 = a11�1 + a12�2 + · · · + a1m�m
...
xn = an1�1 + an2�2 + · · · + anm�m
Como vemos, a partir de una base de W obtenemos automáticamente las ecuaciones paramétricas.
Veamos con unos ejemplos cómo pasar de las ecuaciones paramétricas a las implícitas y a la inversa.
Ejemplo 9. Ecuaciones paramétricas y cartesianas.
1.5. SUMA E INTERSECCIÓN DE SUBESPACIOS. SUMA DIRECTA.
Definición 7. (Intersección de subespacios vectoriales)
Sean U y W subespacios vectoriales de V . La intersección de U y W, U \W, es el conjunto
U \W = {v 2 V tal que v 2 U y v 2 W}
Propiedades.
1. U \ W es un subespacio vectorial de V . En general, tendremos que la intersección de cualquier
familia de subespacios vectoriales de V , Ti Ui, es un subespacio vectorial de V .
2. Si U y W son subespacios vectoriales de Kn, las ecuaciones cartesianas de U \ W serán las
ecuaciones resultantes de unir las de U y las de W.
Ejemplo 10. Intersección de subespacios vectoriales. Ecuaciones.
Definición 8. (Suma de subespacios vectoriales)
Dados U,W subespacios vectoriales de V , llamamos suma de U y W, denotada por U + W, al
conjunto
U +W = {u + w tal que u 2 U,w 2 W}
Propiedades.
1. U + W es un subespacio vectorial de V que contiene al conjunto U [ W. De hecho, es el menor
subespacio vectorial que contiene a U [W, esto es, U +W = L(U [W).
2. De manera análoga se puede definir la suma de cualquier familia de subespacios vectoriales {Ui} de V como Pi Ui = L(Si Ui).
3. (Fórmula de las dimensiones) Si V es de dimensión finita y U,W son subespacios vectoriales
suyos, entonces dim(U +W) = dim(U) + dim(W) − dim(U \W).
Ejemplo 11. Suma de subespacios vectoriales. Ecuaciones.
4
Definición 9. (Suma directa de dos subespacios)
Un espacio vectorial V es suma directa de los subespacios U,W, escrito V = U�W, si U \W = {¯0 } y V = U +W.
Es fácil probar que V = U � W si y sólo si cada vector v 2 V se escribe de modo único como
v = u + w para ciertos u 2 U y w 2 W.
Ejemplo 12. Suma directa.
También es posible definir la suma directa para más de dos subespacios vectoriales. Decimos que V
es suma directa de los subespacios vectoriales U1, . . . ,Un, escrito V = U1�U2�· · ·�Un, si todo vector
v 2 V se puede escribir de modo único como v = u1 +u2 +· · ·+un con ui 2 Ui para todo i = 1, . . . , n.
De manera equivalente, V = U1 � U2 � · · · � Un si:
1. V = L(U1 [ · · · [ Un) y
2. Ui \Pj6=i Uj = {¯0 }.
1.6. COORDENADAS Y CAMBIO DE BASE.
A continuación desarrollamos la herramienta que nos permitirá trabajar en un K-espacio vectorial
V de dimensión finita n como si estuvieramos en Kn.
Definición 10. (Coordenadas de un vector respecto de una base)
Dado un K-espacio vectorial V de dimensión finita n y dada una base B = {e1, . . . , en}, cada vector
x 2 V tiene una única expresión en función de los vectores de B de la forma
x = x1e1 + · · · + xnen
Llamaremos a (x1, . . . , xn) 2 Kn coordenadas de x respecto de la base B y lo representaremos por
xB = (x1, . . . , xn).
Propiedades. Sea V un K-espacio vectorial de dimensión finita n y sea B una base de V . Si x, y 2
V tienen coordenadas (x1, . . . , xn) e (y1, . . . , yn) respecto de B, esto es, xB = (x1, . . . , xn), yB =
(y1, . . . , yn), entonces:
1. [x + y]B = (x1 + y1, . . . , xn + yn).
2. [ax]B = (ax1, . . . , axn).
3. Dado un conjunto de vectores S = {v1, . . . , vr} de V , tendremos que S es l.i., l.d., sistema de
generadores o base de V si y sólo si lo son sus vectores de coordenadas respecto de B en Kn.
Ejemplo 13. Coordenadas.
Dado un espacio vectorial V de dimensión finita n y dadas dos bases distintas
B = {e1, . . . , en} y B0 = {e01, . . . , e0n}
queremos determinar la relación entre las coordenadas de un mismo vector x respecto de las dos bases.
Consideremos las coordenadas de los vectores de B0 en la base B:
e01 = a11e1 + a21e2 + · · · + an1en
...
e0n = a1ne1 + a2ne2 + · · · + annen
5
Sea x 2 V con coordenadas xB = (x1, . . . , xn) y xB0 = (x01, . . . , x0n) respecto de las bases B y B0,
esto es,
x1e1 + · · · + xnen = x = x01e01 + · · · + x0ne0n
Entonces
x1e1 + · · · + xnen = x01(a11e1 + · · · + an1en) + · · · + x0n(a1ne1 + · · · + annen)
Reordenando términos queda
x1e1 + · · · + xnen = (a11x01 + · · · + a1nx0n)e1 + · · · + (an1x01 + · · · + annx0n)en
De modo que
8>
<>
:
x1 = a11x01 + · · · + a1nx0n
...
xn = an1x01 + · · · + annx0n
Estas son las ecuaciones de cambio de base de B0 a B. Si P es la matriz
P =0B@
a11 · · · a1n
...
. . .
...
an1 · · · ann
1CA
entonces tenemos que xB = PxB0 , esto es,
0B@
x1
...
xn
1CA
=0B@
a11 · · · a1n
...
. . .
...
an1 · · · ann
1CA
0B@
x01...
x0n
1CA
Decimos que ésta es la ecuación matricial del cambio de base. A la matriz P se la llama matriz de
cambio de base de B0 a B o matriz de paso, escribiéndose P = M(B0,B), y nos permite determinar las
coordenadas de un vector x en la base B a partir de sus coordenadas en la base B0. Obsérvese que las
columnas de P son las coordenadas de los vectores de B0 respecto de B. Además, P es regular y por
tanto xB0 = P−1xB, fórmula que nos da las coordenadas de un vector x en la base B0 a partir de sus
coordenadas en la base B. Escribimos P−1 = M(B,B0)
Ejemplo 14. Cambio de base.
6