CLASIFICACION DE LAS MATRICES POR SU ORDEN

MATRICES TRIANGULARES

Si en una matriz cuadrada es:

aij = 0 , "i esmenor que j

se dice que la matriz es triangular superior.

La que sigue es una matriz triangular superior de orden 4:

Si en una matriz cuadrada es:

aij = 0 , "i>j

se dice que la matriz es triangular inferior.

La que sigue es una matriz triangular inferior de orden 4:

MATRIZ DIAGONAL

Se llama matriz diagonal a toda matriz que es simultáneamente triangular superior y triangular inferior.

Es inmediato que, en una matriz diagonal, es

aij = 0 , "i¹j .

El siguiente es un ejemplo de matriz diagonal:

MATRIZ ESCALAR

Se llama matriz escalar a toda matriz diagonal en la que:

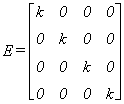
d11=d22=d33= ... = dii= k , siendo k un escalar.

Este es un ejemplo de matriz escalar:

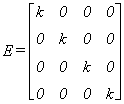
La matriz inversa

Sabemos ya multiplicar matrices y hemos visto algunas de las propiedades de esta operacion.
Recordemos, en primer lugar, que no siempre es posible efect´uar la multiplicacion de dos matrices, y en segundo lugar, que aunque sea posible hacer esta multiplicacion, en general no es conmutativo, es decir A·B es distinto de B·A.
En el caso particular de que tratemos con matrices cuadradas del mismo orden A y B, es claro que podemos efectuar los productos A·B y B·A, que daran como resultado otra matriz del mismo orden, aunque, como ya se ha dicho, las matrices resultantes seran, en general, distintas.
Sabemos tambien que el elemento neutro del producto de matrices es la matriz identidad In.
Por analogıa con el caso de los numeros reales, podemos plantearnos la siguiente cuestion:
Si tenemos un numero real, por ejemplo el 2, podemos interesarnos en buscar el inverso del 2 para el producto, es decir un n´umero real x tal que 2·x = 1, el producto de 2 por x sea igual al elemento neutro, el 1.
Evidentemente, en el caso de los n´umeros reales es bien facil despejar x para obtener, en nuestro caso, que x = 1/2, es decir, el inverso de un numero real es otro numero que multiplicado por el da el elemento neutro, el 1.
Todo numero real, salvo el 0, tiene inverso.
Trasladando esto a las matrices, nos podemos plantear si dada una matriz cuadrada A de orden n, cualquiera, existe su inversa X para el producto de matrices,tal que
A ・ X = In
es decir, el producto de A por su inversa produce el elemento neutro matricial, la matriz identidad In.
Sin embargo, hay algunas diferencias con respecto al caso de los numeros reales:
1) No podemos “despejar” la matriz X del modo X = In /A , porque no hemos definido la division de matrices.
2) No todas las matrices cuadradas no nulas tienen matriz “inversa” (sea lo que sea, por analogıa
con los numeros).
Definamos, en primer lugar, el termino de matriz inversa:
Dada una matriz cuadrada de orden n , A, se dice que A es invertible (o que posee inversa o que es no singular o que es regular ), si existe otra matriz del mismo orden, denominada matriz inversa de A y representada por A−1 y tal que:
A ・ A−1 = In y A−1 ・ A = In
Si A no tiene inversa, se dice que es singular o no invertible.